Treasure/Numbering the Hours

by Kathy (Wagner) Muhs ’73, Assistant Professor of Mathematics

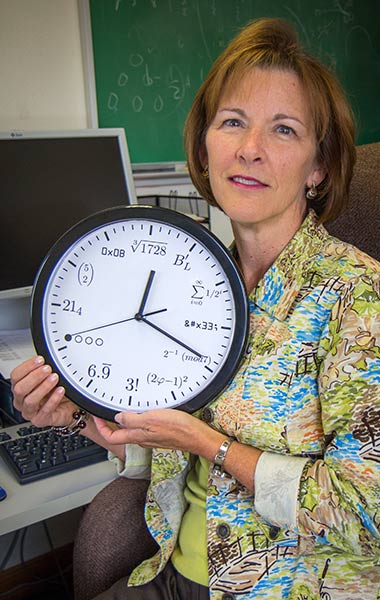
Every issue, we invite one member of the college community to share their delight in an object found on campus. Here, Kathy (Wagner) Huhs '73 (Mathematics) speaks to a clock in her office made up of mathematical symbols. It reminds her of the beauty found in math, and the certainty and comfort of alway arriving at a "right answer." 

It’s hard to decide on my favorite time of day, but I think it might be seven o’clock. Or perhaps it’s five … . These days, I keep time by mathematical symbols, thanks to the clock that hangs opposite my desk.It attracts plenty of comments. Prospective students tend to get pretty excited about it, especially because they recognize some of the math. There is at least one notation that everyone can get: That’s three factorial, or 3*2*1 = 6 (at 6 o’clock).

Eight o’clock is expressed in the binary system. Isn’t that cool? Three o’clock is in ASCII notation – my colleague Bonnie McVey ’82 (Computer Science) was ableto explain that one to me. 

And there’s one time of day that I don’t understand myself – yet. I know that one o’clock is Legendre’s Constant, which relates to prime numbers. I looked up the formula, and I accept it ­­– but I can’t show that it works out. One day I will spend some more time with it! There is so much about math that any mathematician may not know. But the great thing about math is that once something is proven, it cannot be unproven. 

I do particularly like seven o’clock. Seven o’clock illustrates the density of mathematics; that 6.99 repeating infinitely is really the same number as 7. It’s the most elegant notation on the clock, I think, and it’s philosophical as well as mathematical. 

Five o’clock relates to the golden ratio that occurs so frequently in art. The proportions of the Parthenon depend on it, and the proportions of the human body do, too. The golden ratio is an irrational number – it never stops and is non-repeating, like π or the square root of 2. It is represented by the symbol φ.

Actually, I really like most of the notations on my clock. There’s such beauty to the proofs in mathematics – to be able to go from here to there, with nice logical reasoning all the way. You can work through something from multiple directions and you’ll always end up in the same spot. I knew early on that math was for me. I love the fact that you can always arrive at a “right answer.”


Nov. 19, 2013